Unravel Policy Gradients and REINFORCE

This time, we are going to keep ourselves busy with another family of Reinforcement learning algorithms, called policy-based methods. If you recall, there are two main groups of techniques when it comes to model-free Reinforcement Learning.

• Value-Based

• Policy-Based

We analyze the first ones in two previous articles where we talked about Q-learning and Deep Q Networks and different improvement on the basic models such as Double Deep Q Networks and Prioritized Replay. Check them out here and here.

Let’s do a quick rewind. Remember that we frame our problems as Markov Decision Processes and that our goal is to find the best Policy, which is a mapping from states to actions. In other words, we want to know what the action with the maximum expected reward from a given state is. In value-based methods, we achieve that by finding or approximating the Value function and then extract the Policy. What if we completely ditch the value part and find directly the Policy. This is what Policy-based methods do.

Don’t get me wrong. Q-learning and Deep Q networks are great, and they are used in plenty application, but Policy-based methods offer some different advantages:

• They converge more easily to a local or global maximum and they don’t suffer from oscillation

• They are highly effective in high-dimensional or continuous spaces

• They can learn stochastic policies (Stochastic policies give a probability distribution over actions and not a deterministic action. They used in stochastic environments, which they modeled as Partially Observable Markov Decision Processes where we do not know for sure the result of each action)

Hold on a minute. I told about convergence, local maximum, continuous space, stochasticity. What’s going on in here?

Well, the thing is that Policy based reinforcement learning is an optimization problem. But what does this mean?

We have a policy (π) with some parameters theta (θ) that outputs a probability distribution over actions. We want to find the best theta that produces the best policy. But how we evaluate if a policy is good or bad? We use a policy objective function J(θ), which most often is the expected accumulative reward. Also, the objective function varies whether we have episodic or continuing environments.

So here we are, with an optimization problem in our hands. All we have to do is find the parameters theta (θ) that maximizes J(θ) and we have our optimal policy.

The first approach is to use a brute force technique and check the whole policy space. Hmm, not so good.

The second approach is to use a direct search in the policy space or a subset of it. And here we introduce the term of Policy Search. In fact, there are two families of algorithms that we can use. Let’s call them:

• Gradient free

• Gradient-based

Think of any algorithm you have ever used to solve an optimization task, which does not use derivatives. That’s a gradient-free method and most of them can be used in our case. Some examples include:

• Hill climbing is a random iterative local search

• Simplex: a popular linear programming algorithm (if you dig linear algebra check him out)

• Simulated annealing, which moves across different states based on some probability.

• Evolutionary algorithms that simulate the process of physical evolution. They start from a random state represented as a genome and through crossover, mutation and physical selection they find the strongest generation (or the maximum value). The whole “Survival of the fittest” concept wrapped in an algorithm.

The second family of methods uses Gradient Descent or to be more accurate Gradient Ascent.

In (vanilla) gradient descent, we:

1. Initialize the parameters theta

2. Generate the next episode

3. Get long-term reward

4. Update theta based on reward for all time steps

5. Repeat

But there is a small issue. Can we compute the gradient theta in an analytical form? Because if we can’t, the whole process goes to the trash. It turns out that we can with a little trick. We have to assume that policy is differentiable whenever it is non-zero and to use logarithms. Moreover we define the state-action trajectory (τ) as a sequence of states, actions and rewards: τ = (s0,a0,r0, s1,a1,r1…, st,at,rt).

I think that’s enough math for one day. The result, of course, is that we have the gradient in an analytical form and we can now apply our algorithm.

The algorithm described so far (with a slight difference) is called REINFORCE or Monte Carlo policy gradient. The difference from vanilla policy gradients is that we got rid of expectation in the reward as it is not very practical. Instead, we use stochastic gradient descent to update the theta. We sample from the expectation to calculate the reward for the episode and then update the parameters for each step of the episode. It’s quite a straightforward algorithm.

Ok, let’s simplify all those things. You can think policy gradients as so:

For every episode that we got a positive reward, the algorithm will increase the probability of those actions in the future. Similarly, for negative rewards, the algorithms will decrease the probability of the actions. As a result, in time, the actions that lead to negative results are slowly going to be filtered out and those with positive results will become more and more likely. That’s it. If you want to remember one thing from the whole article, this is it. That’s the essence of policy gradients. The only thing that changes every time is how we compute the reward, what policy do we choose (Softmax, Gaussian etc..) and how do we update the parameters.

Now let’s move on.

REINFORCE is, as mentioned, a stochastic gradient descent algorithm. Taking that into consideration, a question comes to mind. Why not use Neural Networks to approximate the policy and update the theta?

Bingo!!

It is time to introduce neural networks into the equation:

We can, of course, use pretty much any machine learning model to approximate the policy function (π), but we use a neural network such as a Convolutional Network because we like Deep Learning. A famous example is an agent that learns to play the game of Pong using Policy gradients and Neural Networks. In that example, a network receives as input frames from the game and outputs a probability of going up or down.

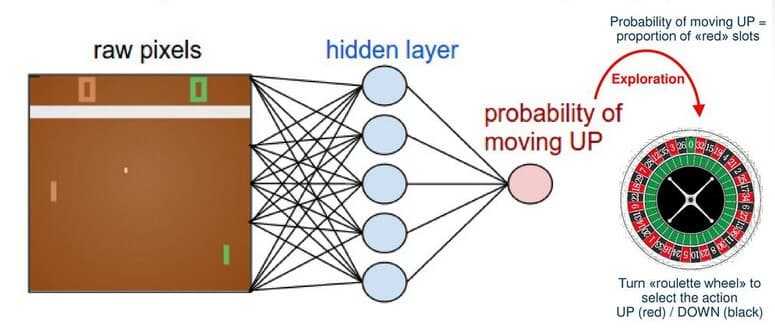http://karpathy.github.io/2016/05/31/rl/

We will try to do something similar using the gym environment by OpenAI.

class REINFORCEAgent:

    # approximate policy using Neural Network
    # state is input and probability of each action is output of network
    def build_model(self):
        model = Sequential()
        model.add(Dense(self.hidden1, input_dim=self.state_size, activation='relu', kernel_initializer='glorot_uniform'))
        model.add(Dense(self.hidden2, activation='relu', kernel_initializer='glorot_uniform'))
        model.add(Dense(self.action_size, activation='softmax', kernel_initializer='glorot_uniform'))
        model.compile(loss="categorical_crossentropy", optimizer=Adam(lr=self.learning_rate))
        return model

    # using the output of policy network, pick action stochastically
    def get_action(self, state):
        policy = self.model.predict(state, batch_size=1).flatten()
        return np.random.choice(self.action_size, 1, p=policy)[0]

    # Agent uses sample returns for evaluating policy
    def discount_rewards(self, rewards):
        discounted_rewards = np.zeros_like(rewards)
        running_add = 0
        for t in reversed(range(0, len(rewards))):
            running_add = running_add * self.discount_factor + rewards[t]
            discounted_rewards[t] = running_add
        return discounted_rewards

    # update policy network every episode
    def train_model(self):
        episode_length = len(self.states)

        discounted_rewards = self.discount_rewards(self.rewards)
        discounted_rewards -= np.mean(discounted_rewards)
        discounted_rewards /= np.std(discounted_rewards)

        update_inputs = np.zeros((episode_length, self.state_size))
        advantages = np.zeros((episode_length, self.action_size))

        for i in range(episode_length):
            update_inputs[i] = self.states[i]
            advantages[i][self.actions[i]] = discounted_rewards[i]

        self.model.fit(update_inputs, advantages, epochs=1, verbose=0)


env = gym.make('CartPole-v1')
state_size = env.observation_space.shape[0]
action_size = env.action_space.n
scores, episodes = [], []

agent = REINFORCEAgent(state_size, action_size)

for e in range(EPISODES):
    done = False
    score = 0
    state = env.reset()
    state = np.reshape(state, [1, state_size])

    while not done:
        if agent.render:
            env.render()

        # get action for the current state and go one step in environment
        action = agent.get_action(state)
        next_state, reward, done, info = env.step(action)
        next_state = np.reshape(next_state, [1, state_size])
        reward = reward if not done or score == 499 else -100

        # save the sample <s, a, r> to the memory
        agent.append_sample(state, action, reward)

        score += reward
        state = next_state

        if done:
            # every episode, agent learns from sample returns
            agent.train_model()
            score = score if score == 500 else score + 100
            scores.append(score)
            episodes.append(e)

You can see that the isn't trivial. We define the neural network model , the monte carlo sampling, the training process and then we let the agent to learn by interacting with the environment and update the weight at the end of each episode.

For more material on Policy Gradients, I highly suggest the Advanced AI: Deep Reinforcement Learning Course in Python on Udemy. It covers everything you need to know from Deep Q Learning to Policy Gradients and Actor critics.

But policy gradients have their own drawbacks. The most important is that they have a high variance and it can be notoriously difficult to stabilize the model parameters.

Do you wannna know how we solve this? Keep in touch...

(Hint: its actor critic models)

Deep Learning in Production Book 📖

Learn how to build, train, deploy, scale and maintain deep learning models. Understand ML infrastructure and MLOps using hands-on examples.

Learn more

* Disclosure: Please note that some of the links above might be affiliate links, and at no additional cost to you, we will earn a commission if you decide to make a purchase after clicking through.