Q-targets, Double DQN and Dueling DQN

Hello again,

Today’s topic is … well, the same as the last one. Q Learning and Deep Q Networks. Last time, we explained what Q Learning is and how to use the Bellman equation to find the Q-values and as a result the optimal policy. Later, we introduced Deep Q Networks and how instead of computing all the values of the Q-table, we let a Deep Neural Network learn to approximate them.

Deep Q Networks take as input the state of the environment and output a Q value for each possible action. The maximum Q value determines, which action the agent will perform. The training of the agents uses as loss the TD Error, which is the difference between the maximum possible value for the next state and the current prediction of the Q-value (as the Bellman equation suggests). As a result, we manage to approximate the Q-tables using a Neural Network.

So far so good. But of course, there are a few problems that arise. It’s just the way scientific research is moving forward. And of course, we have come up with some great solutions.

Moving Q-Targets

The first problem is what is called moving Q-targets. As we saw, the first component of the TD Error (TD stands for Temporal Difference) is the Q-Target and it is calculated as the immediate reward plus the discounted max Q-value for the next state. When we train our agent, we update the weights accordingly to the TD Error. But the same weights apply to both the target and the predicted value. You see the problem?

\Delta w=\alpha\left[\left(R+\gamma \max _{a} \hat{Q}\left(s^{\prime}, a, w\right)\right)-\hat{Q}(s, a, w)\right] \nabla_{w} \hat{Q}(s, a, w)

We move the output closer to the target, but we also move the target. So, we end up chasing the target and we get a highly oscillated training process. Wouldn’t be great to keep the target fixed as we train the network. Well, DeepMind did exactly that.

Instead of using one Neural Network, it uses two. Yes, you heard that right! (like one wasn’t enough already).

One as the main Deep Q Network and a second one (called Target Network) to update exclusively and periodically the weights of the target. This technique is called Fixed Q-Targets. In fact, the weights are fixed for the largest part of the training and they updated only once in a while.

class DQNAgent:
    def __init__(self, state_size, action_size):
        self.model = self._build_model()
        self.target_model = self._build_model()
        self.update_target_model()

    def update_target_model(self):
        # copy weights from model to target_model
        self.target_model.set_weights(self.model.get_weights())

Maximization Bias

Maximization bias is the tendency of Deep Q Networks to overestimate both the value and the action-value (Q) functions. Why does it happen? Think that if for some reason the network overestimates a Q value for an action, that action will be chosen as the go-to action for the next step and the same overestimated value will be used as a target value. In other words, there is no way to evaluate if the action with the max value is actually the best action. How to solve this? The answer is a very interesting method and is called:

Double Deep Q Network

To address maximization bias, we use two Deep Q Networks.

On the one hand, the DQN is responsible for the selection of the next action (the one with the maximum value) as always.
On the other hand, the Target network is responsible for the evaluation of that action.

The trick is that the target value is not automatically produced by the maximum Q-value, but by the Target network. In other words, we call forth the Target network to calculate the target Q value of taking that action at the next state. And as a side effect, we also solve the moving target problem. Neat right? Two birds with one stone. By decoupling the action selection from the target Q-value generation, we are able to substantially reduce the overestimation, and train faster and more reliably.

def train_model(self):
        if len(self.memory) < self.train_start:
            return
        batch_size = min(self.batch_size, len(self.memory))
        mini_batch = random.sample(self.memory, batch_size)

        update_input = np.zeros((batch_size, self.state_size))
        update_target = np.zeros((batch_size, self.state_size))
        action, reward, done = [], [], []

        for i in range(batch_size):
            update_input[i] = mini_batch[i][0]
            action.append(mini_batch[i][1])
            reward.append(mini_batch[i][2])
            update_target[i] = mini_batch[i][3]
            done.append(mini_batch[i][4])

        target = self.model.predict(update_input)
        target_next = self.model.predict(update_target) #DQN
        target_val = self.target_model.predict(update_target) #Target model

        for i in range(self.batch_size):
            if done[i]:
                target[i][action[i]] = reward[i]
            else:
                # selection of action is from model
                # update is from target model
                a = np.argmax(target_next[i])
                target[i][action[i]] = reward[i] + self.discount_factor * (target_val[i][a])

        self.model.fit(update_input, target, batch_size=self.batch_size,epochs=1, verbose=0)

You think that’s it? Sorry to let you down. We are going to take this even further. What now? Are you going to add a third Neural Network? Haha!!

Well kind of. Who’s laughing now?

Dueling Deep Q Networks

Let’s refresh the basis of Q Learning first. Q values correspond to a metric of how good an action is for a particular state right? That’s why it is an action-value function. The metric is nothing more the expected return of that action from the state. Q values can, in fact, be decomposed into two pieces: the state Value function V(s) and the advantage value A(s, a). And yes, we just introduce one more function:

Q(s, a)=V(s)+A(s, a)

Advantage function captures how better an action is compared to the others at a given state, while as we know the value function captures how good it is to be at this state. The whole idea behind Dueling Q Networks relies on the representation of the Q function as a sum of the Value and the advantage function. We simply have two networks to learn each part of the sum and then we aggregate their outputs.

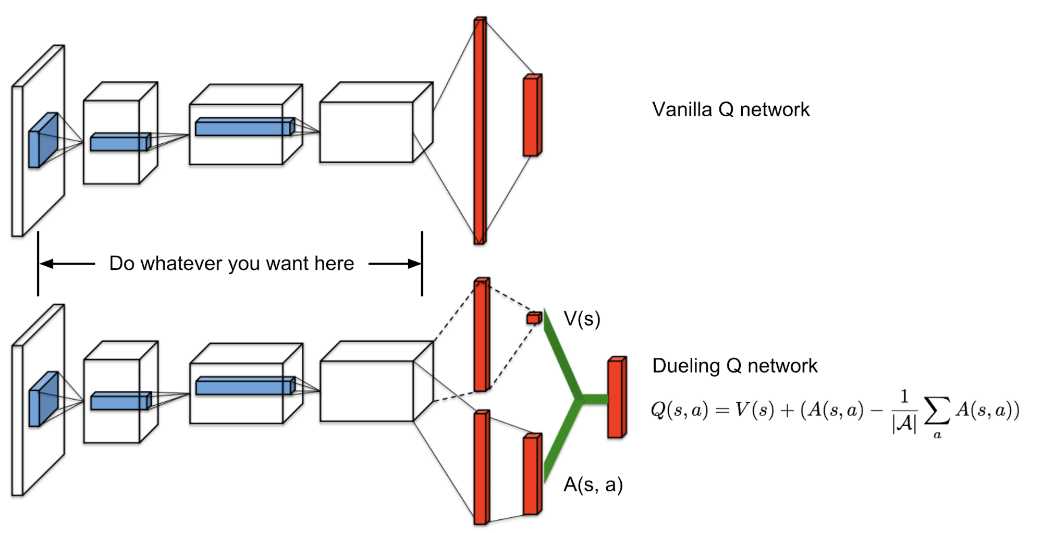Dueling Network Architectures for Deep Reinforcement Learning

Do we earn something by doing that? Of course, we do. The agents in now able to evaluate a state without caring about the effect of each action from that state. Meaning that the features that determined whether a state is good or nor are not necessarily the same as the features that evaluate an action. And it may not need to care for actions at all. It is not uncommon to have actions from a state that do not affect the environment at all. So why take them into consideration?

* Quick note: If you take a closer look at the image, you will see that to aggregate the output of the two networks we do not simply add them. The reason behind that is the issue of identifiability. If we have the Q, we can’t find the V and A. So, we can’t back propagate. Instead, we choose to use the mean advantage as a baseline (the subtracted term).

def build_model(self):
        input = Input(shape=self.state_size)
        shared = Conv2D(32, (8, 8), strides=(4, 4), activation='relu')(input)
        shared = Conv2D(64, (4, 4), strides=(2, 2), activation='relu')(shared)
        shared = Conv2D(64, (3, 3), strides=(1, 1), activation='relu')(shared)
        flatten = Flatten()(shared)

        # network separate state value and advantages
        advantage_fc = Dense(512, activation='relu')(flatten)
        advantage = Dense(self.action_size)(advantage_fc)
        advantage = Lambda(lambda a: a[:, :] - K.mean(a[:, :], keepdims=True),
                           output_shape=(self.action_size,))(advantage)

        value_fc = Dense(512, activation='relu')(flatten)
        value =  Dense(1)(value_fc)
        value = Lambda(lambda s: K.expand_dims(s[:, 0], -1),
                       output_shape=(self.action_size,))(value)

        q_value = merge([value, advantage], mode='sum')
        model = Model(inputs=input, outputs=q_value)
        model.summary()

        return model

Last but not least, we have on more issue to discuss and it has to do with optimizing the experience replay.

Prioritized Experience Replay

Do you remember that experience replay is when we replay to the agent random past experiences every now and then to prevent him from forgetting them? If you don’t, now you do. But some experiences may be more significant than others. As a result, we should prioritize them to be replayed. To do just that, instead of sampling randomly (from a uniform distribution), we sample using a priority. As priority we define the magnitude of the TD Error (plus some constant to avoid zero probability for an experience to be chosen).

p=|\delta|+\varepsilon

Central idea: The highest the error between the prediction and the target, the more urgent is to learn about it.

And to ensure that we won’t always replay the same experience, we add some stochasticity and we are all set. Also, for complexity's shake we save the experiences in a binary tree called SumTree.

P(i)=\frac{p_{i}^{\alpha}}{\sum_{k} p_{k}^{\alpha}}

from SumTree import SumTree

class PER:  # stored as ( s, a, r, s_ ) in SumTree
    e = 0.01
    a = 0.6
    def __init__(self, capacity):
        self.tree = SumTree(capacity)

    def _getPriority(self, error):
        return (error + self.e) ** self.a

    def add(self, error, sample):
        p = self._getPriority(error)
        self.tree.add(p, sample)

    def sample(self, n):
        batch = []
        segment = self.tree.total() / n

        for i in range(n):
            a = segment * i
            b = segment * (i + 1)

            s = random.uniform(a, b)
            (idx, p, data) = self.tree.get(s)
            batch.append((idx, data))

        return batch

    def update(self, idx, error):
        p = self._getPriority(error)
        self.tree.update(idx, p)

That was a lot. A lot of new information, a lot of new improvements. But just think what we can combine all of them together. And we do it.

I tried to give a summary of the most important recent efforts in the field, backed by some intuitive thought and some math. This is why Reinforcement Learning is so important to learn. There is so much potential and so many capabilities for enhancements that you just can’t ignore the fact that is going to be the big player in AI (if it already isn’t). But that’s why is so hard to learn and to keep up with it.

If you need to dive deeper, I highly suggest the Advanced AI: Deep Reinforcement Learning Course in Python on Udemy.

Next time, we will introduce Policy Gradients and the REINFORCE algorithm

All we have to do is keep learning …

* Disclosure: Please note that some of the links above might be affiliate links, and at no additional cost to you, we will earn a commission if you decide to make a purchase after clicking through.

Q-targets, Double DQN and Dueling DQN

Moving Q-Targets

Maximization Bias

Double Deep Q Network

Dueling Deep Q Networks

Prioritized Experience Replay

Deep Learning in Production Book 📖

Learn how to build, train, deploy, scale and maintain deep learning models. Understand ML infrastructure and MLOps using hands-on examples.

Q-targets, Double DQN and Dueling DQN

Moving Q-Targets

Maximization Bias

Double Deep Q Network

Download our free ebook on Deep Reinforcement Learning

We combined all of Reinforcement Learning articles into a single pdf. So if you don't have time to read the whole article or you want a pdf version to read offline, click the button below

Dueling Deep Q Networks

Prioritized Experience Replay

Deep Learning in Production Book 📖

Learn how to build, train, deploy, scale and maintain deep learning models. Understand ML infrastructure and MLOps using hands-on examples.