Explain Neural Arithmetic Logic Units (NALU)

So Deepmind released a new paper a few days ago with the title Neural Arithmetic Logic Units (NALU). After the victory of AlphaGo against the top Go player in the world, every new paper from DeepMind comes with an excitement in the AI community. But this time all that fuzz is totally worth it. Alright, then what is NALU and what is its purpose?

Why we need NALUs?

Neural Networks have proven to have the uncanny ability to learn complex functions from any kind of data, whether it is numbers, images or sound. But they have a significant flaw: they can’t count. What I mean by is that they can't output values outside the range of training data.

For example, if we have a training set with range from 0 to 100, the output will also be between that same range. It does not matter which activation function or what optimization technique we use, the output will always be inside that range. So, if we want to build a counter with a neural network, we can’t pass it the following data [0,1,2,3,4,5] and expect to output 6. Below is an interesting graph what shows exactly that:

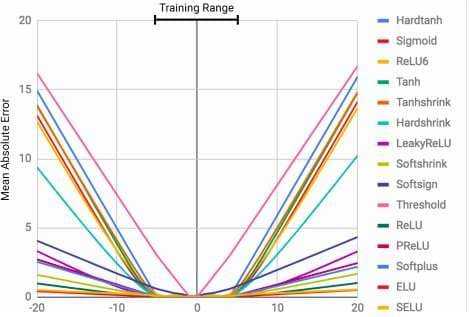(Neural Arithmetic Logic Units)[https://arxiv.org/pdf/1808.00508.pdf] : MLPs learn the identity function only for the range values they are trained on. The mean error ramps up severely both below and above the range of numbers seen during training. Credit: Trask et al.

What is NALU?

You could argue that this is a somewhat significant limitation of deep learning and I agree with you. Here is where NALU come in place. NALU use a careful combination of gates and extend the Neural Accumulator model (NAC). NAC is in fact a linear transformation and can accumulate inputs additively.

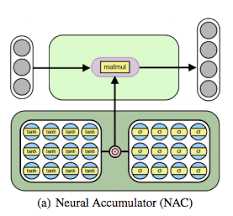(Neural Arithmetic Logic Units)[https://arxiv.org/pdf/1808.00508.pdf]

NALU extends the addition and subtraction functionality of NACs and can represent multiplications and divisions. It consists of two NAC cells (one for addition and one for multiplication) interpolated by a learned sigmoidal gate.

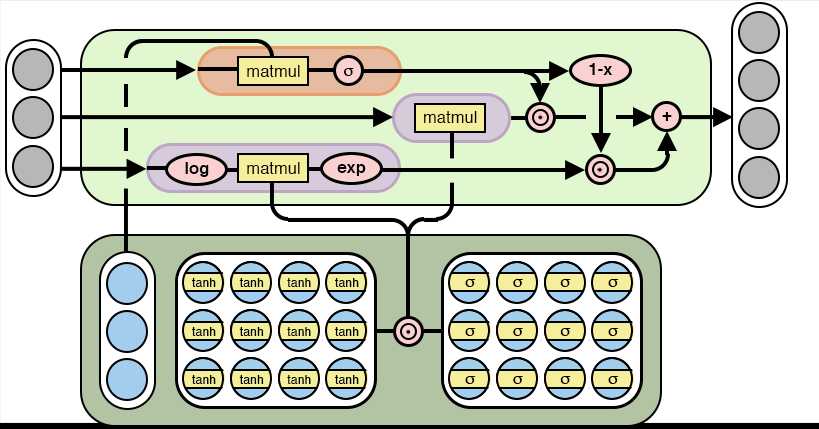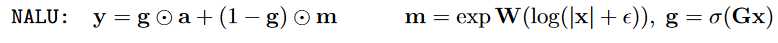(Neural Arithmetic Logic Units)[https://arxiv.org/pdf/1808.00508.pdf]

Clearly it is not very easy to explain why the gates have this particular structure because it is a result of complex mathematical principles and tools. Kudos to the researchers. However, what is important is that those units can now use in any known model from convolutional networks to autoencoders and enhance their capabilities. Examples of practical applications that already have examined by the authors and provide rally promising results are:

Learn Simple Arithmetic functions
Count how many hand-written characters appear on an image
Translate text-number expressions to numeric values
Track Time in a Grid-World Environment

For more info about the above, please read the paper. And you should because we are talking about some exciting stuff.

Implementation in Python

Let’s now try to build a NALU using Tensorflow and Python and test for ourselves how well they work. We have the equations, we have a nice graphic representation. It shouldn't be that difficult. Right? And it really isn’t.

If we follow the mathematical expressions appeared above we have:

import tensorflow as tf

def NALU(prev_layer, num_outputs):
    eps=1e-7
    shape = (int(prev_layer.shape[-1]),num_outputs)

    # NAC cell
    W_hat = tf.Variable(tf.truncated_normal(shape, stddev=0.02))
    M_hat = tf.Variable(tf.truncated_normal(shape, stddev=0.02))
    W = tf.tanh(W_hat) * tf.sigmoid(M_hat)
    a = tf.matmul(prev_layer, W)
    G = tf.Variable(tf.truncated_normal(shape, stddev=0.02))

    # NALU
    m = tf.exp(tf.matmul(tf.log(tf.abs(prev_layer) + eps), W))
    g = tf.sigmoid(tf.matmul(prev_layer, G))
    out = g * a + (1 - g) * m
    return out

Well thats it! Now let's construct a simple neural network exclusively by NALU's and use it to learn a simple mathematical function. First lets build some dummy data to train and test our model:

arithmetic_functions={
'add': lambda x,y :x+y,
}

def get_data(N, op):
    split = 4
    X_train = np.random.rand(N, 10)*10
    #to be mutually exclusive
    a = X_train[:, :split].sum(1)
    b = X_train[:, split:].sum(1)
    Y_train = op(a, b)[:, None]
    print(X_train.shape)
    print(Y_train.shape)

    X_test = np.random.rand(N, 10)*100
    #to be mutually exclusive
    a = X_test[:, :split].sum(1)
    b = X_test[:, split:].sum(1)
    Y_test = op(a, b)[:, None]
    print(X_test.shape)
    print(Y_test.shape)

    return (X_train,Y_train),(X_test,Y_test)

Notice that the test set has a much bigger range than the train set. The purpose of that diffrenece is to test how well the model can extrapolate. Now we have to create the tensorflow session an run the backpropagation algorithm.

tf.reset_default_graph()
    train_examples=10000

    (X_train,Y_train),(X_test,Y_test)=get_data(train_examples,arithmetic_functions['add'])
    X = tf.placeholder(tf.float32, shape=[train_examples, 10])
    Y = tf.placeholder(tf.float32, shape=[train_examples, 1])

    X_1=NALU(X,2)
    Y_pred=NALU(X_1,1)

    loss = tf.nn.l2_loss(Y_pred - Y) # NALU uses mse
    optimizer = tf.train.AdamOptimizer(0.1)
    train_op = optimizer.minimize(loss)

    with tf.Session() as session:

        session.run(tf.global_variables_initializer())
        for ep in range(50000):
            _,pred,l = session.run([train_op, Y_pred, loss],
                    feed_dict={X: X_train, Y: Y_train})
            if ep % 1000 == 0:
                print('epoch {0}, loss: {1}'.format(ep,l))

        _,test_predictions,test_loss = session.run([train_op, Y_pred,loss],feed_dict={X:X_test,Y:Y_test})

    print(test_loss) #8.575397e-05

The loss(the mean square error) on test set turns out to be 8.575397e-05. Amazing! Its practically zero. Note that the test data had a different range of the training data, thus we can conclude the extrapolation of F(x,y)=x+y is almost perfect. We can,of course, test that in other simple functions. The results will be similarly good.

It is clear that the applications of Neural Arithmetic Logic Units (NALU) are practically endless ,as they can be used in literally every existing model to improve its performance and extend their capabilities beyond the range of the training data.

* Disclosure: Please note that some of the links above might be affiliate links, and at no additional cost to you, we will earn a commission if you decide to make a purchase after clicking through.

Explain Neural Arithmetic Logic Units (NALU)

Why we need NALUs?

What is NALU?

Implementation in Python

Deep Learning in Production Book 📖

Learn how to build, train, deploy, scale and maintain deep learning models. Understand ML infrastructure and MLOps using hands-on examples.