How Transformers work in deep learning and NLP: an intuitive introduction

The famous paper “Attention is all you need” in 2017 changed the way we were thinking about attention. With enough data, matrix multiplications, linear layers, and layer normalization we can perform state-of-the-art-machine-translation.

Nonetheless, 2020 was definitely the year of transformers! From natural language now they are into computer vision tasks. How did we go from attention to self-attention? Why does the transformer work so damn well? What are the critical components for its success?

Read on and find out!

In my opinion, transformers are not so hard to grasp. It's the combination of all the surrounding concepts that may be confusing, including attention. That’s why we will slowly build around all the fundamental concepts.

With Recurrent Neural Networks (RNN’s) we used to treat sequences sequentially to keep the order of the sentence in place. To satisfy that design, each RNN component (layer) needs the previous (hidden) output. As such, stacked LSTM computations were performed sequentially.

Until transformers came out! The fundamental building block of a transformer is self-attention. To begin with, we need to get over sequential processing, recurrency, and LSTM’s!

How?

By simply changing the input representation!

For a complete book to guide your learning on NLP, take a look at the "Deep Learning for Natural Language Processing" book. Use the code aisummer35 to get an exclusive 35% discount from your favorite AI blog :)

Representing the input sentence

Sets and tokenization

The transformer revolution started with a simple question: Why don’t we feed the entire input sequence? No dependencies between hidden states! That might be cool!

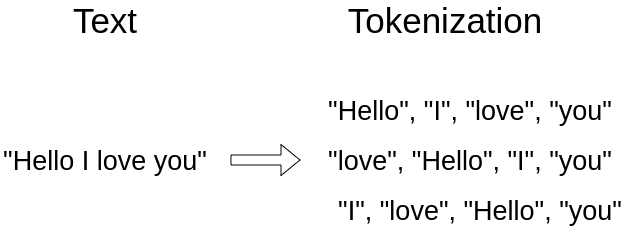
As an example the sentence “hello, I love you”:

This processing step is usually called tokenization and it's the first out of three steps before we feed the input in the model.

So instead of a sequence of elements, we now have a set.

Sets are a collection of distinct elements, where the arrangement of the elements in the set does not matter.

In other words, the order is irrelevant. We denote the input set as $\textbf{X}= { \textbf{x}_1, \textbf{x}_2, \textbf{x}_3 … , \textbf{x}_N}$ where $\textbf{x} \in R^{N \times d_{in}}$. The elements of the sequence $x_i$ are referred to as tokens.

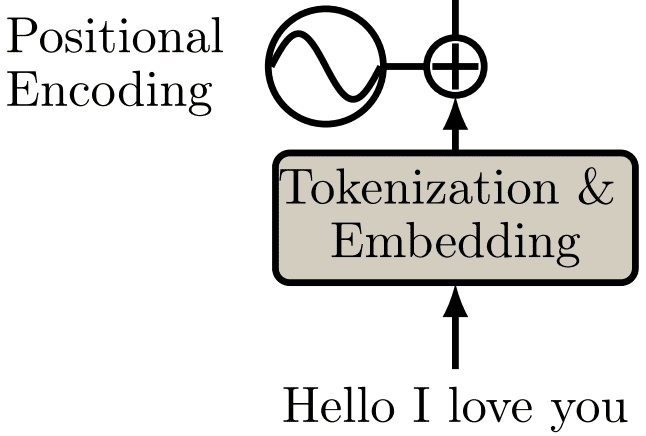
After tokenization, we project words in a distributed geometrical space, or simply build word embeddings.

Word Embeddings

In general, an embedding is a representation of a symbol (word, character, sentence) in a distributed low-dimensional space of continuous-valued vectors.

Words are not discrete symbols. They are strongly correlated with each other. That’s why when we project them in a continuous euclidean space we can find associations between them.

Then, dependent on the task, we can push word embeddings further away or keep them close together.

Ideally, an embedding captures the semantics of the input by placing semantically similar inputs close together in the embedding space.

In natural language, we can find similar word meanings or even similar syntactic structures (i.e. objects get clustered together). In any case, when you project them in 2D or 3D space you can visually identify some clusters. I found this 3D illustration interesting:

To gain a practical understanding of word-embeddings, try playing around with this notebook.

Moving on, we will devise a funky trick to provide some notion of order in the set.

Positional encodings

When you convert a sequence into a set (tokenization), you lose the notion of order.

Can you find the order of words (tokens) from the sequence: “Hello I love you”? Probably yes! But what about 30 unordered words?

Remember, machine learning is all about scale. The neural network certainly cannot understand any order in a set.

Since transformers process sequences as sets, they are, in theory, permutation invariant.

Let’s help them have a sense of order by slightly altering the embeddings based on the position. Officially, positional encoding is a set of small constants, which are added to the word embedding vector before the first self-attention layer.

So if the same word appears in a different position, the actual representation will be slightly different, depending on where it appears in the input sentence.

Source

In the transformer paper, the authors came up with the sinusoidal function for the positional encoding. The sine function tells the model to pay attention to a particular wavelength $\lambda$. Given a signal $y(x) = \sin (k x)$ the wavelength will be $k = \frac{2 \pi}{\lambda}$. In our case the $\lambda$ will be dependent on the position in the sentence. $i$ is used to distinguish between odd and even positions.

Mathematically:

For the record, $512= d_{model}$, which is the dimensionality of the embedding vectors.

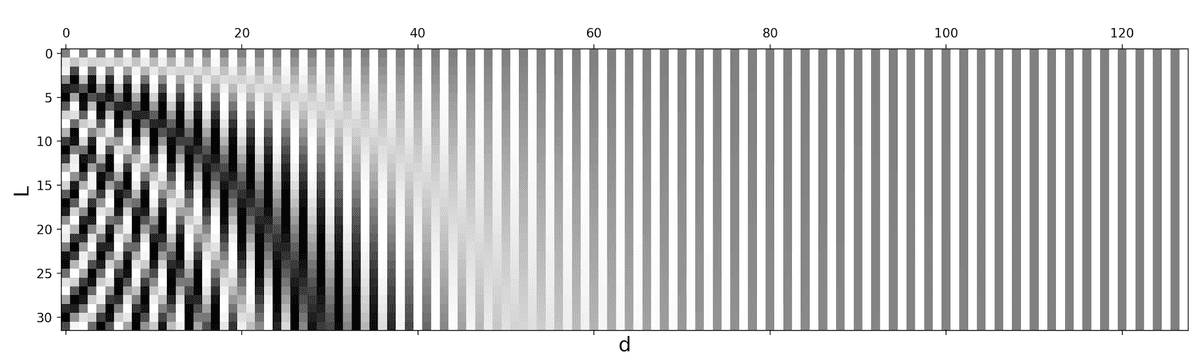A 2D Vizualization of a positional encoding. Image from The Transformer Family by Lil'Log

This is in contrast to recurrent models, where we have an order but we are struggling to pay attention to tokens that are not close enough.

Fundamental concepts of the Transformer

This section provides some necessary background. Feel free to skip it and jump in self-attention straight on if you already feel comfortable with the concepts.

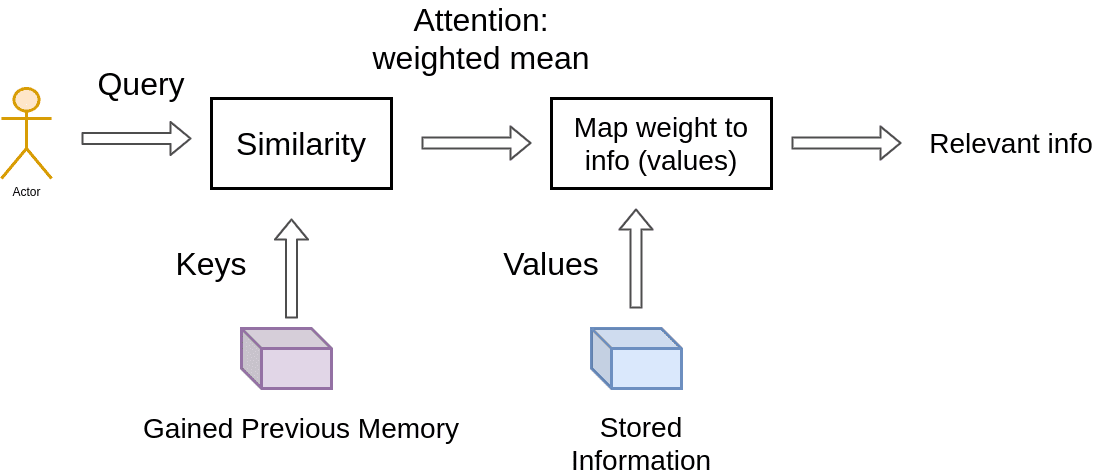
Feature-based attention: The Key, Value, and Query

Key-value-query concepts come from information retrieval systems. I found it extremely helpful to clarify these concepts first.

Let’s start with an example of searching for a video on youtube.

When you search (query) for a particular video, the search engine will map your query against a set of keys (video title, description, etc.) associated with possible stored videos. Then the algorithm will present you the best-matched videos (values). This is the foundation of content/feature-based lookup.

Bringing this idea closer to the transformer’s attention we have something like this:

In the single video retrieval, the attention is the choice of the video with a maximum relevance score.

But we can relax this idea. To this end, the main difference between attention and retrieval systems is that we introduce a more abstract and smooth notion of ‘retrieving’ an object. By defining a degree of similarity (weight) between our representations (videos for youtube) we can weight our query.

Instead of choosing where to look according to the position within a sequence, we now attend to the content that we wanna look at!

So, by moving one step forward, we further split the data into key-value pairs.

We use the keys to define the attention weights to look at the data and the values as the information that we will actually get.

For the so-called mapping, we need to quantify similarity, that we will be seeing next.

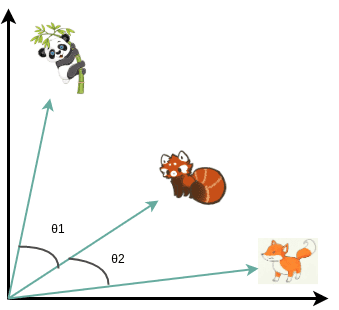
Vector similarity in high dimensional spaces

In geometry, the inner vector product is interpreted as a vector projection. One way to define vector similarity is by computing the normalized inner product. In low dimensional space, like the 2D example below, this would correspond to the cosine value.

Mathematically:

We can associate the similarity between vectors that represent anything (i.e. animals) by calculating the scaled dot product, namely the cosine of the angle.

In transformers, this is the most basic operation and is handled by the self-attention layer as we’ll see.

Self-Attention: The Transformer encoder

What is self-attention?

“Self-attention, sometimes called intra-attention, is an attention mechanism relating different positions of a single sequence in order to compute a representation of the sequence.” ~ Ashish Vaswani et al. [2] from Google Brain.

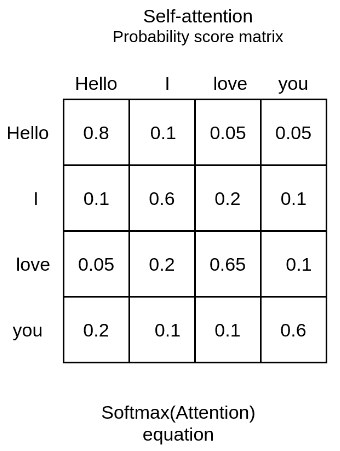
Self-attention enables us to find correlations between different words of the input indicating the syntactic and contextual structure of the sentence.

Let’s take the input sequence “Hello I love you” for example. A trained self-attention layer will associate the word “love” with the words ‘I” and “you” with a higher weight than the word “Hello”. From linguistics, we know that these words share a subject-verb-object relationship and that’s an intuitive way to understand what self-attention will capture.

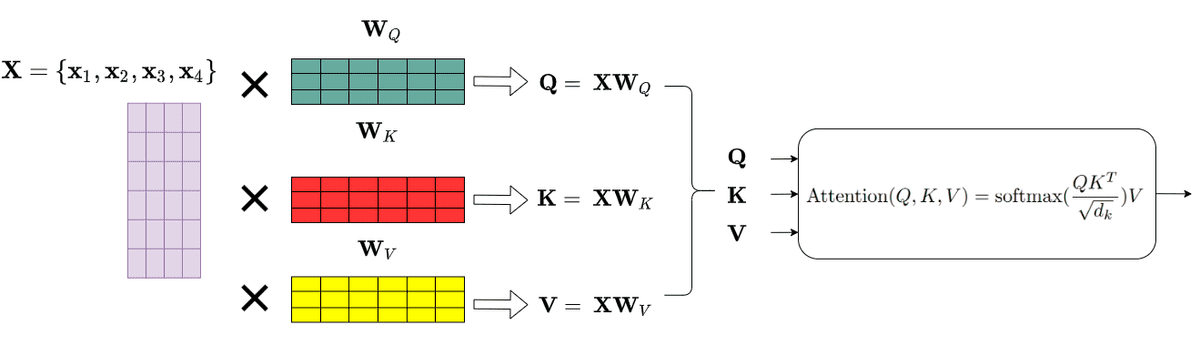
In practice, the Transformer uses 3 different representations: the Queries, Keys and Values of the embedding matrix. This can easily be done by multiplying our input $\textbf{X} \in R^{N \times d_{model} }$ with 3 different weight matrices $\textbf{W}_Q$, $\textbf{W}_K$ and $\textbf{W}_V \in R^{ d_{model} \times d_{k}}$ . In essence, it's just a matrix multiplication in the original word embeddings. The resulted dimension will be smaller: $d_{k} < d_{model}$

Having the Query, Value and Key matrices, we can now apply the self-attention layer as:

In the original paper, the scaled dot-product attention was chosen as a scoring function to represent the correlation between two words (the attention weight). Note that we can also utilize another similarity function. The $\sqrt{d_{k}}$ is here simply as a scaling factor to make sure that the gradients won’t explode.

Following the database-query paradigm we introduced before, this term simply finds the similarity of the searching query with an entry in a database. Finally, we apply a softmax function to get the final attention weights as a probability distribution.

Remember that we have distinguished the Keys ($K$) from the Values ($V$) as distinct representations. Thus, the final representation is the self-attention matrix $\operatorname{softmax}\left(\frac{\textbf{Q} \textbf{K}^{T}}{\sqrt{d_{k}}}\right)$ multiplied with the Value ($V$) matrix.

Personally, I like to think of the attention matrix as where to look and the Value matrix as what I actually want to get.

Notice any differences between vector similarity?

First, we have matrices instead of vectors and as a result matrix multiplications. Second, we don’t scale down by the vector magnitude but by the matrix size ($d_k$), which is the number of words in a sentence! Sentence size varies :)

What would we do next?

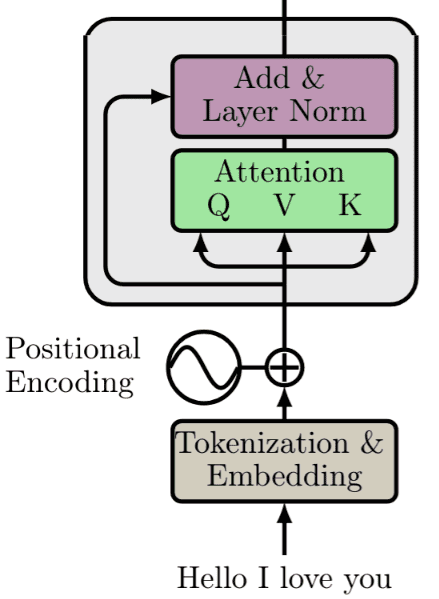
Normalization and short skip connections, similar to processing a tensor after convolution or recurrency.

Short residual skip connections

In language, there is a significant notion of a wider understanding of the world and our ability to combine ideas. Humans extensively utilize these top-down influences (our expectations) to combine words in different contexts. In a very rough manner, skip connections give a transformer a tiny ability to allow the representations of different levels of processing to interact.

With the forming of multiple paths, we can “pass” our higher-level understanding of the last layers to the previous layers. This allows us to re-modulate how we understand the input. Again, this is the same idea as human top-down understanding, which is nothing more than expectations.

For a more detailed and general overview, advice our article on skip connections.

Layer Normalization

Next, let’s open the Layer Norm black box.

In Layer Normalization (LN), the mean and variance are computed across channels and spatial dims. In language, each word is a vector. Since we are dealing with vectors we only have one spatial dimension.

In a 4D tensor with merged spatial dimensions, we can visualize this with the following figure:

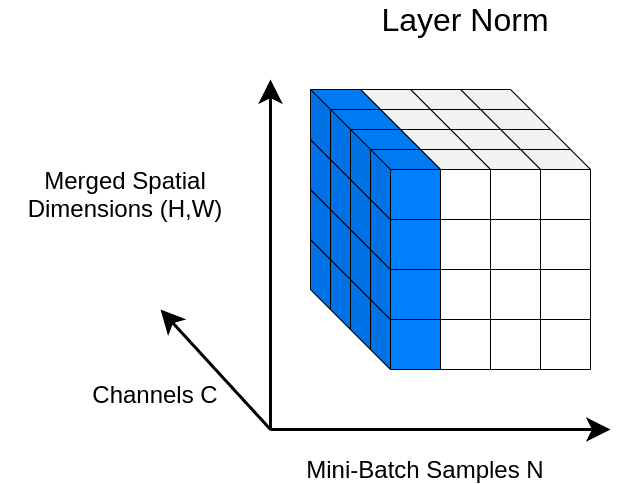An illustration of Layer Norm.

After applying a normalization layer and forming a residual skip connection we are here:

Source

Even though this could be a stand-alone building block, the creators of the transformer add another MLP (see below) on top and renormalize it along with another skip connection.

The MLP: 2 linear layers + non linear activation

Here, I want to clarify the linear transformation layer. There are a lot of fancy ways to say trainable matrix multiplication; linear layer (PyTorch), dense layer (Keras), feed-forward layer (old ML books), fully connected layer. For this tutorial, we will simply say linear layer which is:

Where $\textbf{W}$ is a matrix and $\textbf{y} , \textbf{x}, \textbf{b}$ are vectors.

In fact, they add two linear layers with dropout and non-linearities in between. This is usually refered to as MLP, which stands for multilayer perceptron.

import torch.nn as nn
dim = 512
dim_linear_block = 512*4

mlp = nn.Sequential(
    nn.Linear(dim, dim_linear_block),
    nn.ReLU,
    nn.Dropout(dropout),
    nn.Linear(dim_linear_block, dim),
    nn.Dropout(dropout))

The main intuition is that they project the output of self-attention in a higher dimensional space (X4 in the paper). This solves bad initializations and rank collapse. We will depict it in the diagrams simply as Linear.

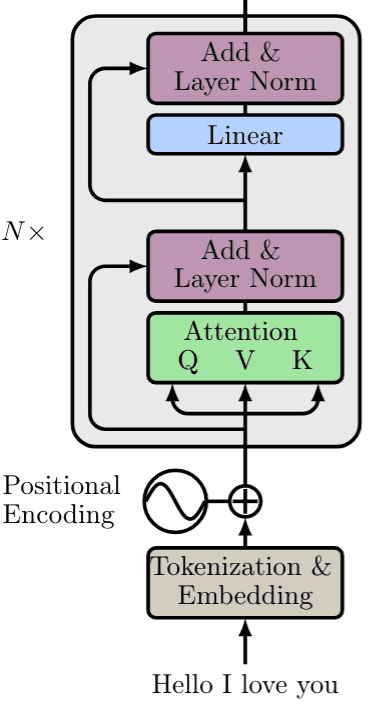
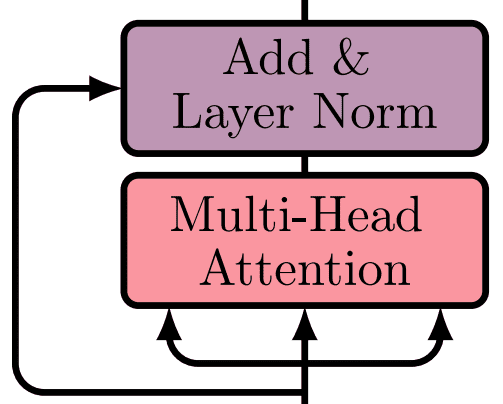
This is the encoder part of the transformer with N such building blocks, as depicted below:

Source

Actually this is almost the encoder of the transformer. There is one difference. Multi-head attention.

The core building block: Multi-head attention and parallel implementation

In the original paper, the authors expand on the idea of self-attention to multi-head attention. In essence, we run through the attention mechanism several times.

Each time, we map the independent set of Key, Query, Value matrices into different lower dimensional spaces and compute the attention there (the output is called a “head”). The mapping is achieved by multiplying each matrix with a separate weight matrix, denoted as $\textbf{W}_{i}^{K} , \textbf{W}_{i}^{Q} \in R^{d_{model} \times d_{k} }$ and $, \textbf{W}_{i}^{V} \in R^{d_{model} \times d_{k}}$

To compensate for the extra complexity, the output vector size is divided by the number of heads. Specifically, in the vanilla transformer, they use $d_{model}=512$ and $h=8$ heads, which gives us vector representations of 64. Now, the model has multiple independent paths (ways) to understand the input.

The heads are then concatenated and transformed using a square weight matrix $\textbf{W}^{O} \in R^{d_{model} \times d_{model}}$, since $d_{model}=h d_{k}$

Putting it all together we get:

where again:

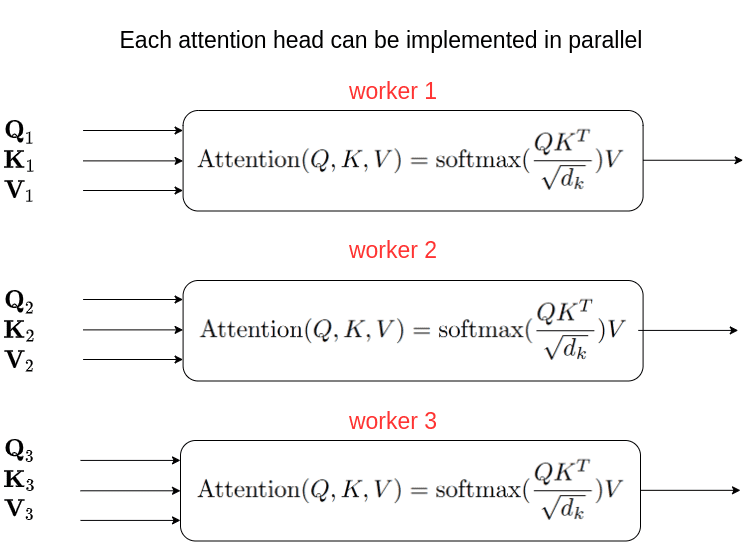
Since heads are independent from each other, we can perform the self-attention computation in parallel on different workers:

But why go through all this trouble?

The intuition behind multi-head attention is that it allows us to attend to different parts of the sequence differently each time. This practically means that:

• The model can better capture positional information because each head will attend to different segments of the input. The combination of them will give us a more robust representation.

• Each head will capture different contextual information as well, by correlating words in a unique manner.

To quote the original paper [2]:

“Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this.”

We will depict Multi-head self-attention in our diagrams like this:

Source

To get your mind around multihead attention, feel free to check out our Pytorch implementation using the einsum notation.

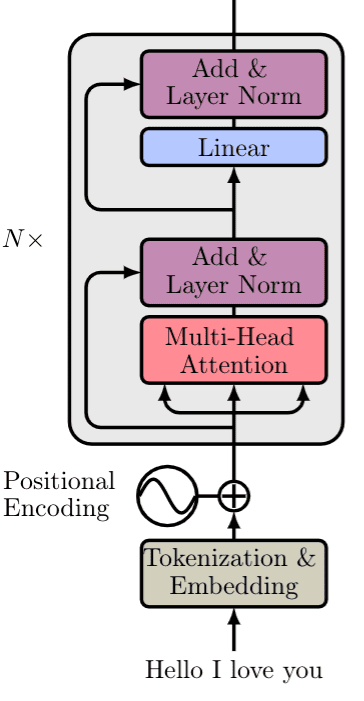
Sum up: the Transformer encoder

To process a sentence we need these 3 steps:

1. Word embeddings of the input sentence are computed simultaneously.

2. Positional encodings are then applied to each embedding resulting in word vectors that also include positional information.

3. The word vectors are passed to the first encoder block.

Each block consists of the following layers in the same order:

1. A multi-head self-attention layer to find correlations between all pairs of words in a sentence.

2. A normalization layer

3. A residual connection around the previous two sublayers

4. An MLP (remember: 2 linear layers + non linear activation)

5. A second normalization layer

6. A second residual connection

Note that the above block can be replicated several times to form the Encoder. In the original paper, the encoder composed of 6 identical blocks.

Source

A small detail: Even though the original paper states that the normalization layer is applied after the skip connection, in practice the exact opposite is established. This is usually terms as "prenorm", meaning before the skip connection. On the other hand when Layer norm is used after the skip connection is called "postnorm". My advice is don't bother so much about it at this stage.

Let’s see what might be different in the decoder part.

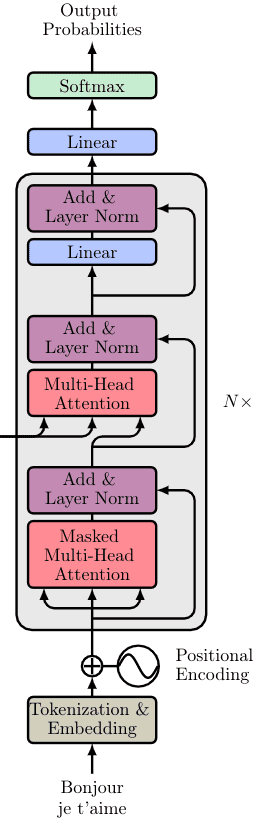
Transformer decoder: what is different?

The decoder consists of all the aforementioned components plus two novel ones. As before:

1. The output sequence is fed in its entirety and word embeddings are computed

2. Positional encoding are again applied

3. And the vectors are passed to the first Decoder block

Each decoder block includes:

1. A Masked multi-head self-attention layer

2. A normalization layer followed by a residual connection

3. A new multi-head attention layer (known as Encoder-Decoder attention)

4. A second normalization layer and a residual connection

5. A linear layer and a third residual connection

The decoder block appears again 6 times. The final output is transformed through a final linear layer and the output probabilities are calculated with the standard softmax function.

Source

The output probabilities predict the next token in the output sentence. How? In essence, we assign a probability to each word in the French language and we simply keep the one with the highest score.

To put things into perspective, the original model was trained on the WMT 2014 English-French dataset consisting of 36M sentences and 32000 tokens.

While most concepts of the decoder are already familiar, there are two more that we need to discuss. Let’s start with the Masked multi-head self-attention layer.

Masked Multi-head attention

In case you haven’t realized, in the decoding stage, we predict one word (token) after another. In such NLP problems like machine translation, sequential token prediction is unavoidable. As a result, the self-attention layer needs to be modified in order to consider only the output sentence that has been generated so far.

In our translation example, the input of the decoder on the third pass will be “Bonjour”, “je” … …”.

As you can tell, the difference here is that we don’t know the whole sentence because it hasn’t been produced yet. That’s why we need to disregard the unknown words. Otherwise, the model would just copy the next word! To achieve this, we mask the next word embeddings (by setting them to $-\inf$).

Mathematically we have:

where the matrix M (mask) consists of zeros and $-\inf$.

Zeros will become ones with the exponential while infinities become zeros.

This effectively has the same effect as removing the corresponding connection. The remaining principles are exactly the same as the encoder’s attention. And once again, we can implement them in parallel to speed up the computations.

Obviously, the mask will change for every new token we compute.

Encoder-Decoder attention: where the magic happens

This is actually where the decoder processes the encoded representation. The attention matrix generated by the encoder is passed to another attention layer alongside the result of the previous Masked Multi-head attention block.

The intuition behind the encoder-decoder attention layer is to combine the input and output sentence. The encoder’s output encapsulates the final embedding of the input sentence. It is like our database. So we will use the encoder output to produce the Key and Value matrices. On the other hand, the output of the Masked Multi-head attention block contains the so far generated new sentence and is represented as the Query matrix in the attention layer. Again, it is the “search” in the database.

The encoder-decoder attention is trained to associate the input sentence with the corresponding output word.

It will eventually determine how related each English word is with respect to the French words. This is essentially where the mapping between English and French is happening.

Notice that the output of the last block of the encoder will be used in each decoder block.

Intuitions on why transformers work so damn well

1. Distributed and independent representations at each block: Each transformer block has $h=8$ contextualized representations. Intuitively, you can think of it as the multiple feature maps of a convolution layer that capture different features from the image. The difference with convolutions is that here we have multiple views (linear reprojections) to other spaces. This is of course possible by initially representing words as vectors in a euclidean space (and not as discrete symbols).

2. The meaning heavily depends on the context: This is exactly what self-attention is all about! We associate relationships between word representation expressed by the attention weights. There is no notion of locality since we naturally let the model make global associations.

3. Multiple encoder and decoder blocks: With more layers, the model makes more abstract representations. Similar to stacking recurrent or convolution blocks we can stack multiple transformer blocks. The first block associates word-vector pairs, the second pairs of pairs, the third of pairs of pairs of pairs, and so on. In parallel, the multiple heads focus on different segments of the pairs. This is analogous to the receptive field but in terms of pairs of distributed representations.

4. Combination of high and low-level information: with skip-connections of course! They enable top-down understanding to flow back with the multiple gradient paths that flow backward.

Self-attention VS linear layers VS convolutions

What is the difference between attention and a feedforward layer? Don't linear layers do exactly the same operations to an input vector as attention?

Good question! The answer is no if you delve deep into the concepts.

You see the values of the self-attention weights are computed on the fly. They are data-dependent dynamic weights because they change dynamically in response to the data (fast weights).

For example, each word in the translated sequence (Bonjour, je t’aime) will attend differently with respect to the input.

On the other hand, the weights of a feedforward (linear) layer change very slowly with stochastic gradient descent. In convolutions, we further constrict the (slow) weight to have a fixed size, namely the kernel size.

Conclusion

If you felt that you gained a new insight from this article, we kindly ask you to share it with your colleagues, friends, or on your social page. As a follow-up reading, take a look at how you can implement a transformer with multi-head self-attention from scratch!

Acknowledgments

For the visualizations, I used the awesome repo of Renato Negrinho. Most of my enlightenment on the transformer architecture came from the lecture of Felix Hill [1]. It is one of the very few resources where you can learn more about intuitions rather than pure math.

Cited as

@article{adaloglou2021transformer,
    title   = "Transformers in Computer Vision",
    author  = "Adaloglou, Nikolas",
    journal = "https://theaisummer.com/",
    year    = "2021",
    howpublished = {https://github.com/The-AI-Summer/self-attention-cv},
  }

References

[1] DeepMind’s deep learning videos 2020 with UCL, Lecture: Deep Learning for Natural Language Processing, Felix Hill

[2] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. In Advances in neural information processing systems (pp. 5998-6008).

[3] Stanford CS224N: NLP with Deep Learning , Winter 2019 , Lecture 14 – Transformers and Self-Attention

[4] CS480/680 Lecture 19: Attention and Transformer Networks by Pascal Poupart

[5] Neural Machine Translation and Models with Attention - Stanford

Deep Learning in Production Book 📖

Learn how to build, train, deploy, scale and maintain deep learning models. Understand ML infrastructure and MLOps using hands-on examples.

Learn more

* Disclosure: Please note that some of the links above might be affiliate links, and at no additional cost to you, we will earn a commission if you decide to make a purchase after clicking through.