Understanding einsum for Deep learning: implement a transformer with multi-head self-attention from scratch

If you are a machine learning researcher/engineer nowadays you should definitely be aware of einsum operations!

Personally speaking, I used to give up understanding git repos because of einsum operations. The reason: even though I felt pretty comfortable with tensor operations einsum was not in my arsenal.

Long story short, I decided I want to get familiar with the einsum notation. Since I am particularly interested in transformers and self-attention in computer vision, I have a huge playground.

In this article, I will extensively try to familiarize myself with einsum (in Pytorch), and in parallel, I will implement the famous self-attention layer, and finally a vanilla Transformer.

The code is totally educational! I haven’t trained any large self-attention model yet but I plan to. Truthfully speaking, I learned much more in the process than I initially expected.

If you want to delve into the theory first, feel free to check my articles on attention and transformer.

If not, let the game begin!

The code of this tutorial is available on GitHub. Show your support with a star!

Why einsum?

First, einsum notation is all about elegant and clean code. Many AI industry specialists and researchers use it consistently:

To convince you even more, let’s see an example:

You want to merge 2 dims of a 4D tensor, first and last.

x = x.permute(0, 3, 1, 2)
N, W, C, H = x.shape
x = x.contiguous().view(N * W, C, -1)

This is not the optimal way to code it, but it serves my point!

Personally, this code freaks me out!

It’s a good practice to improve your code’s readability with einsum. In the previous case that would be something like this:

x = einops.rearrange(x, 'b c h w -> (b w) c h')

Neat and clean!

Second reason: if you care about batched implementations of custom layers with multi-dimensional tensors, einsum should definitely be in your arsenal!

Third reason: translating code from PyTorch to TensorFlow or NumPy becomes trivial.

I am completely aware that it takes time to get used to it. That’s why I decided to implement some self-attention mechanisms.

The einsum and einops notation basics

If you know the basics of einsum and einops you may skip this section.

Einsum

To deal with multi-dimensional computations back in 1916 Albert Einstein developed a compact form to indicate summation over some indexes. The so-called Einstein summation convention is what we use when we call einsum.

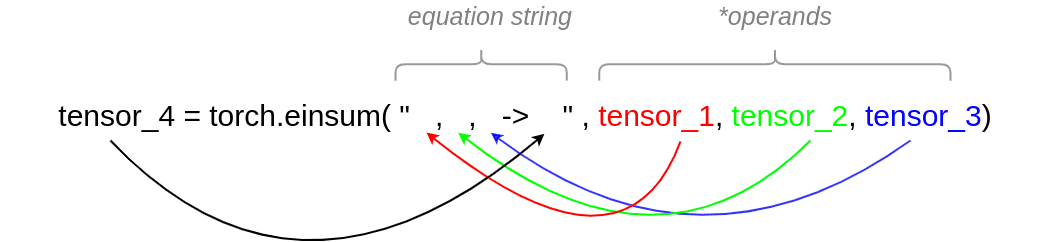
In a nutshell, this is how einsum commands are structured:

Image by Author

We can split the arguments of einsum into two parts:

Equation string: Here is where all the indices will be. Each index will indicate the dimension of the tensor. To do that, we use lowercase letters. For operations that will be performed on an axis of equal dimension on multiple tensors, we must use the same symbol. This provides einsum with the information that we will perform fancy stuff on this dimension. There must be as many commas at the left side of -> as the tensor that we use. I believe that the colored arrows make that clear.

On the right side of -> we have the index of the output of the operation we perform. We need as many indexes as the output dimensions. The letters (indices) that we use on the output must exist on the right side of the equation string.

Operands: We can provide as many tensors as we want. Obviously, the number of tensors must be precisely the same as the left part of the -> equation.

An example: Batch Matrix Multiplication with einsum

Let’s say we have 2 tensors with the following shapes and we want to perform a batch matrix multiplication in Pytorch:

a = torch.randn(10,20,30) # b -> 10, i -> 20, k -> 30
c = torch.randn(10,50,30) # b -> 10, j -> 50, k -> 30

With einsum you can clearly state it with one elegant command:

y1 = torch.einsum('b i k, b j k -> b i j', a , c) # shape [10, 20, 50]

Let’s divide the process of writing the command into steps:

We place out tensors in the second argument as operands
We put a string with the -> symbol
Left to the -> symbol: Since we have two tensors a, c we have to index their dimensions. Both have 3 dims so we have to use symbols for each one of the three dimensions (6 in total). I use the same symbol b for the batch dim (5 in total). Let’s make them 4 (see below why): b, i, k for tensor a and b, j, k for tensor c
For the axes that will be summed due to matrix multiplication, we have to use the same symbol to index both a and c. In that case that will be the index k (4 symbols). That will make clear to einsum that this is the axis that we want to operate on.
Right to the -> symbol: The resulting dimensions based on the operation. We have to use the previous symbols here. This will indicate the shape of the result and einsum will understand that it is a multiplication.

Without einsum, you would have to permute the axes of b and after apply batch matrix multiplication. You also have to remember the command of Pytorch for batch matrix multiplication.

y2 = torch.bmm(a, c.permute(0, 2, 1))

Let’s use the einsum notation to quickly operate on a single tensor.

Einops

Even though einops is a general library, here I will only cover einops.rearrange. It’s been proved extremely useful to me so far.

In einops, the equation string is exactly the same. The argument order is reversed. You specify the tensor or the list of tensors first. The following image may clarify things out:

Image by author

The underscores are for illustration purposes only. We would put symbols in a real example. You can understand from the number of underscores, that this operation will merge some of the two dimensions together (composition). On the left part of the equation string, we have the 4 input dimensions and on the right, only three are remaining.

With einsum, instead, that would probably mean summation over one axis.

In case a list of tensors is provided in rearrange, the first dimension (depicted as underscore) will refer to the length of the list, which is the number of tensors

I also adore the decomposition flexibility of einops. It’s a great illustration of the axes’ length also! Here is an example:

qkv = torch.rand(2,128,3*512) # dummy data for illustration only
# We need to decompose to n=3 tensors q, v, k
# rearrange tensor to [3, batch, tokens, dim] and cast to tuple
q, k, v = tuple(rearrange( qkv , 'b t (d n) -> n b t d ', n=3))

We split - decompose - the axis in 3 equal parts! Note that in order to decompose an axis you need to specify the length of the index/axis.

The tuple command will use the first tensor’s dimension and it will create a tuple of n=3 tensors.

Convention: Throughout this article, I extensively use einops.rearrange when I operate on a single tensor and torch.einsum when I operate on multiple tensors.

Axis indexing rules

The difference with einops is that you can use more than single lowercase letters for indexing a dimension (i.e flattening a 2D tensor: “nikolas , aisummer -> (nikolas aisummer) ’’).

However, you always need to leave some space between the indices of the axis in this way. For convenience, I will leave a space in torch.einsum operations also and I will try to use single letters for indexing.

Finally, if you feel you need more practice with einsum and einops, advise the acknowledgments section.

Now let’s write some code!

After some thinking, I realized that the best way to understand the implementations is to break it down into steps with some math. I also indicate the steps in the code.

Scaled dot product self-attention

The math in steps

Step 1: Create linear projections, given input $\textbf{X} \in R^{batch \times tokens \times dim}$ . The matrix multiplication happens in the $d$ dimension. For NLP, that would be the dimensionality of word embeddings.

$\textbf{Q} = \textbf{X} \textbf{W}_Q$

$\textbf{K} = \textbf{X} \textbf{W}_K$

$\textbf{V} = \textbf{X} \textbf{W}_V$

to_qvk = nn.Linear(dim, dim * 3, bias=False) # init only
# Step 1
qkv = to_qvk(x)  # [batch, tokens, dim*3 ]
# decomposition to q,v,k
q, k, v = tuple(rearrange(qkv, 'b t (d k) -> k b t d ', k=3))

Step 2: Calculate scaled dot product, apply mask, and finally compute softmax in $d$ (last) dimension

$\operatorname{Dot-scores} = \operatorname{softmax}\left(\frac{\textbf{Q} \textbf{K}^{T}}{\sqrt{d_{k}}}\right)$

# Step 2
# Resulting shape: [batch, tokens, tokens]
scaled_dot_prod = torch.einsum('b i d , b j d -> b i j', q, k) * self.scale_factor
if mask is not None:
    assert mask.shape == scaled_dot_prod.shape[1:]
    scaled_dot_prod = scaled_dot_prod.masked_fill(mask, -np.inf)
attention = torch.softmax(scaled_dot_prod, dim=-1)

Step 3: Multiply scores with $\textbf{V}$

$\operatorname{Attention}(\textbf{Q}, \textbf{K}, \textbf{V})=\operatorname{softmax}\left(\frac{\textbf{Q} \textbf{K}^{T}}{\sqrt{d_{k}}}\right) \textbf{V}$

torch.einsum('b i j , b j d -> b i d', attention, v)

Implementation of scaled dot product self-attention

import numpy as np
import torch
from einops import rearrange
from torch import nn


class SelfAttentionAISummer(nn.Module):
    """
    Implementation of plain self attention mechanism with einsum operations
    Paper: https://arxiv.org/abs/1706.03762
    Blog: https://theaisummer.com/transformer/
    """
    def __init__(self, dim):
        """
        Args:
            dim: for NLP it is the dimension of the embedding vector
            the last dimension size that will be provided in forward(x),
            where x is a 3D tensor
        """
        super().__init__()
        # for Step 1
        self.to_qvk = nn.Linear(dim, dim * 3, bias=False)
        # for Step 2
        self.scale_factor = dim ** -0.5  # 1/np.sqrt(dim)

    def forward(self, x, mask=None):
        assert x.dim() == 3, '3D tensor must be provided'

        # Step 1
        qkv = self.to_qvk(x)  # [batch, tokens, dim*3 ]

        # decomposition to q,v,k
        # rearrange tensor to [3, batch, tokens, dim] and cast to tuple
        q, k, v = tuple(rearrange(qkv, 'b t (d k) -> k b t d ', k=3))

        # Step 2
        # Resulting shape: [batch, tokens, tokens]
        scaled_dot_prod = torch.einsum('b i d , b j d -> b i j', q, k) * self.scale_factor

        if mask is not None:
            assert mask.shape == scaled_dot_prod.shape[1:]
            scaled_dot_prod = scaled_dot_prod.masked_fill(mask, -np.inf)

        attention = torch.softmax(scaled_dot_prod, dim=-1)

        # Step 3
        return torch.einsum('b i j , b j d -> b i d', attention, v)

Code explanation

It is important to notice the softmax dimension. Here we used the last one. However, the scaled dot product is a square matrix for each input sequence (tokens x tokens). Someone would argue that we could use the other dimension.

The answer is simple: you have to multiply $\textbf{V}$ in the dimension you apply the softmax. Be careful of that.

Another thing is that we used a single linear layer for the linear projections. This is totally ok since it’s the same operation applied 3 times. We then have to decompose the representation by casting it to q,v,k.

Multi-Head Self-Attention

Let’s see how we can introduce multiple heads in our computations. This type of attention is called Multi-Head Self-Attention (MHSA). Intuitively we will perform multiple computations in a lower-dimensional space (dim_head in the code). The multiple computations are completely independent. It is conceptually similar to batch size. You can think of it as a batch of low-dimensional self-attentions.

In my opinion, this is where the expressive power of the einsum notation will surprise you.

The code in steps

Step 1: Create linear projections $\textbf{Q}, \textbf{K}, \textbf{V}$ per head. The matrix multiplication happens in the $d$ dimension. Instead of $d \times 3$ , now we will project into $dim_{head} \times 3 \times heads$ outputs.

The heads have lower dimensionality $dim_{head} < dim$ , and actually it is common to use $dim_{head} = dim/heads$ .

to_qvk = nn.Linear(dim, dim_head * heads * 3, bias=False) # init only
qkv = self.to_qvk(x)

Step 2: Decompose representations $\textbf{Q}, \textbf{K}, \textbf{V}$ per head.

# Step 2
# decomposition to q,v,k and cast to tuple
# [3, batch, heads, tokens, dim_head]
q, k, v = tuple(rearrange(qkv, 'b t (d k h) -> k b h t d ', k=3, h=self.heads))

Step 3: Calculate scaled dot product, apply the mask, and finally compute softmax in $dim_{head}$ - last dimension. Basically, we just have one more dimension that corresponds to the number of heads. The computation is carried out exactly the same way.

${ \operatorname{dot-prod-head} }_{\mathrm{i}} = \operatorname{softmax}\left(\frac{\textbf{Q}_i \textbf{K}^{T}_i}{\sqrt{d_{k}}}\right)$

# Step 3
# resulted shape will be: [batch, heads, tokens, tokens]
scaled_dot_prod = torch.einsum('b h i d , b h j d -> b h i j', q, k) * self.scale_factor
if mask is not None:
    assert mask.shape == scaled_dot_prod.shape[2:]
    scaled_dot_prod = scaled_dot_prod.masked_fill(mask, -np.inf)
attention = torch.softmax(scaled_dot_prod, dim=-1)

Step 4: Multiply per head dot product scores with $\textbf{V}$

${ head }_{\mathrm{i}} =\operatorname{Attention}(\textbf{Q}_i, \textbf{K}_i, \textbf{V}_i)=\operatorname{softmax}\left(\frac{\textbf{Q}_i \textbf{K}^{T}_i}{\sqrt{d_{k}}}\right) \textbf{V}_i$

# Step 4. Calc result per batch and per head h
out = torch.einsum('b h i j , b h j d -> b h i d', attention, v)

Step 5: Recompose/merge heads (h) with $dim_{head}$ (the dimension of the computations so far)

out = rearrange(out, "b h t d -> b t (h d)")

Step 6: Apply final linear transformation layer $\textbf{W}^{O}$

\text { MultiHead }(\textbf{Q}, \textbf{K}, \textbf{V}) =\text { Concat (head }_{1}, \ldots, \text { head } \left._{\mathrm{h}}\right) \textbf{W}^{O}

\text { where head }_{\mathrm{i}} =\text { Attention }\left(\textbf{Q} \textbf{W}_{i}^{Q}, \textbf{K} \textbf{W}_{i}^{K},\textbf{V} \textbf{W}_{i}^{V}\right)

self.W_0 = nn.Linear( _dim, dim, bias=False) # init only
# Step 6. Apply final linear transformation layer
self.W_0(out)

Implementation of MHSA

import numpy as np
import torch
from einops import rearrange
from torch import nn


class MultiHeadSelfAttentionAISummer(nn.Module):
    def __init__(self, dim, heads=8, dim_head=None):
        """
        Implementation of multi-head attention layer of the original transformer model.
        einsum and einops.rearrange is used whenever possible
        Args:
            dim: token's dimension, i.e. word embedding vector size
            heads: the number of distinct representations to learn
            dim_head: the dim of the head. In general dim_head<dim.
            However, it may not necessary be (dim/heads)
        """
        super().__init__()
        self.dim_head = (int(dim / heads)) if dim_head is None else dim_head
        _dim = self.dim_head * heads
        self.heads = heads
        self.to_qvk = nn.Linear(dim, _dim * 3, bias=False)
        self.W_0 = nn.Linear( _dim, dim, bias=False)
        self.scale_factor = self.dim_head ** -0.5

    def forward(self, x, mask=None):
        assert x.dim() == 3
        # Step 1
        qkv = self.to_qvk(x)  # [batch, tokens, dim*3*heads ]

        # Step 2
        # decomposition to q,v,k and cast to tuple
        # the resulted shape before casting to tuple will be:
        # [3, batch, heads, tokens, dim_head]
        q, k, v = tuple(rearrange(qkv, 'b t (d k h) -> k b h t d ', k=3, h=self.heads))

        # Step 3
        # resulted shape will be: [batch, heads, tokens, tokens]
        scaled_dot_prod = torch.einsum('b h i d , b h j d -> b h i j', q, k) * self.scale_factor

        if mask is not None:
            assert mask.shape == scaled_dot_prod.shape[2:]
            scaled_dot_prod = scaled_dot_prod.masked_fill(mask, -np.inf)

        attention = torch.softmax(scaled_dot_prod, dim=-1)

        # Step 4. Calc result per batch and per head h
        out = torch.einsum('b h i j , b h j d -> b h i d', attention, v)

        # Step 5. Re-compose: merge heads with dim_head d
        out = rearrange(out, "b h t d -> b t (h d)")

        # Step 6. Apply final linear transformation layer
        return self.W_0(out)

TransformerEncoder

In case you forgot, the vanilla transformer looks like this:

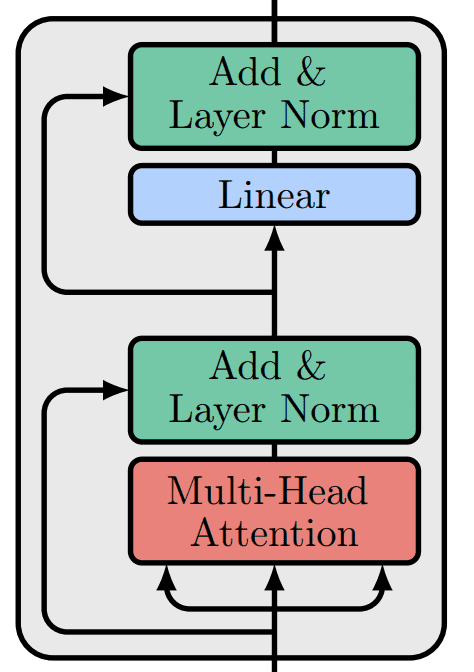Image by Author based on the code of Renato Negrinho

Having a solid code for MHSA, building a Transformer block is as easy as this:

from torch import nn

from .mhsa import MultiHeadSelfAttention


class TransformerBlockAISummer(nn.Module):
   """
   Vanilla transformer block from the original paper "Attention is all you need"
   Detailed analysis: https://theaisummer.com/transformer/
   """

   def __init__(self, dim, heads=8, dim_head=None, dim_linear_block=1024, dropout=0.1):
       """
       Args:
           dim: token's vector length
           heads: number of heads
           dim_head: if none dim/heads is used
           dim_linear_block: the inner projection dim
           dropout: probability of droppping values
       """
       super().__init__()
       self.mhsa = MultiHeadSelfAttention(dim=dim, heads=heads, dim_head=dim_head)
       self.drop = nn.Dropout(dropout)
       self.norm_1 = nn.LayerNorm(dim)
       self.norm_2 = nn.LayerNorm(dim)

       self.linear = nn.Sequential(
           nn.Linear(dim, dim_linear_block),
           nn.ReLU(),
           nn.Dropout(dropout),
           nn.Linear(dim_linear_block, dim),
           nn.Dropout(dropout)
       )

   def forward(self, x, mask=None):
       y = self.norm_1(self.drop(self.mhsa(x, mask)) + x)
       return self.norm_2(self.linear(y) + y)

Since we have extensively covered this architecture, I will let you analyze the code yourself.

Finally, we can stack multiple such blocks together and create our fancy Transformer Encoder:

class TransformerEncoderAISummer(nn.Module):
   def __init__(self, dim, blocks=6, heads=8, dim_head=None):
       super().__init__()
       self.block_list = [TransformerBlock(dim, heads, dim_head) for _ in range(blocks)]
       self.layers = nn.ModuleList(self.block_list)

   def forward(self, x, mask=None):
       for layer in self.layers:
           x = layer(x, mask)
       return x

Homework: build the Vision Transformer :)

Conclusion

It took me some time to solidify my understanding of self-attention and einsum, but it was a fun ride. In the next article, I will try to implement more advanced self-attention blocks for computer vision. Meanwhile, use our Github repository in your next project and let us know how it goes out.

Don’t forget to star our repository to show us your support!

If you feel like your PyTorch fundamentals need some extra practice, learn from the best ones out there. Use the code aisummer35 to get an exclusive 35% discount from your favourite AI blog :)

Acknowledgments

A huge shout out to Alex Rogozhnikov (@arogozhnikov) for the awesome einops lib.

Here is a list of other resources that significantly accelerated my learning on einsum operations, attention, or transformers:

* Disclosure: Please note that some of the links above might be affiliate links, and at no additional cost to you, we will earn a commission if you decide to make a purchase after clicking through.